General aspects
I bet some of you will start shouting that they don’t want any theory, because nobody understands it and they don’t need it anyway. This reaction may be due to the horror you still remember from your school days when you simply had to learn the theory, without ever seeing its practical use. On the other hand, I keep hearing remarks like: "I am a trumpet player, and I’m sure my notation was correct, yet it sounded horrible when played by an alto saxophone. How come?" Not to worry! What I want to show you here starts at ground level... there is absolutely nothing you need to know beforehand. This is important for all musicians and will help those who play an instrument understand what playing with other musicians is really about.
The major scale
Going from one major scale to the next requires several well-defined steps. The basic rule is that each step towards the next note is a semitone step. This creates a fixed pattern for major scales.
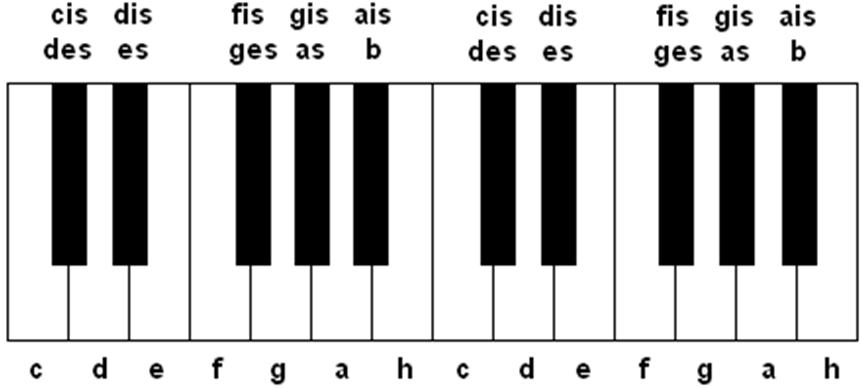
The C major scale is a good case in point. This scale comprises the notes C D E F G A B C, i.e. only white piano keys. Now, there is a note between the C and the D, called C#/Db, meaning that C and D are actually separated by 2 semitones= a whole tone: C-C# and C#-D).
There is no note between the E and the F, and so this step (like the one from B to C) is a semitone step. The structure of the C major scale thus looks as follows:

Any notes that are not part of the C major scale (i.e. all black keys) are indicated by means of an accidental. Raising the C’s pitch by a semitone step turns it into a C#, for instance. Lowering a D by a semitone step turns it into a Db. That is what the "#" and "b" signs are for.
All major scales follow the exact same pattern:
2 whole steps • 1 semitone step • 3 whole steps • 1 semitone step
Intervals
The distance between any two notes is called an "interval". Knowing the intervals is helpful for the construction of additional scales.
C-C#/Db = minor second (1 semitone step)
C-D = major second (1 whole tone step)
C-D#/Eb = minor third (1 ½ steps)
C-E = major third (2 whole steps)
C-F = pure fourth (2 whole steps, 1 semitone step)
C-F#/Gb = augmented fourth/diminished fifth
(also called tritone"”the C and F# are separated by 3 whole-tone steps)
C-G = pure fifth (3 ½ steps)
C-G#/Ab = augmented fifth/minor sixth
C-A = major sixth
C-A#/Bb = minor seventh
C-B = major seventh
C-C = octave
Understanding intervals becomes important when you start analyzing the structure of musical chords. The C major scale is not the only major scale"”there are 11 more major scales. Let us now look at accidentals. Let’s start with the sharps (#).
A major scale based on the G as starting point requires an F# as final semitone step to preserve the "2 whole, 1 semitone, 3 whole, 1 semitone steps" rule. The F is therefore absent from G major scale: it is replaced by the F#. That explains the key signature of the G major scale: one sharp ("#"), which turns the F into an F#. The interval I used to get from C to G is a fifth.
Now let’s use G major as our initial key. The fifth of G is D. The D major scale also uses the F# introduced by the G major key. And there is another note that needs to be altered to ensure that the scale’s last interval is a semitone step. Here, we need to raise C to C#. D major therefore has 2 sharps (#) in its key signature: F# and C#.
Consistently applying this system produces one of music’s most ingenious tools:
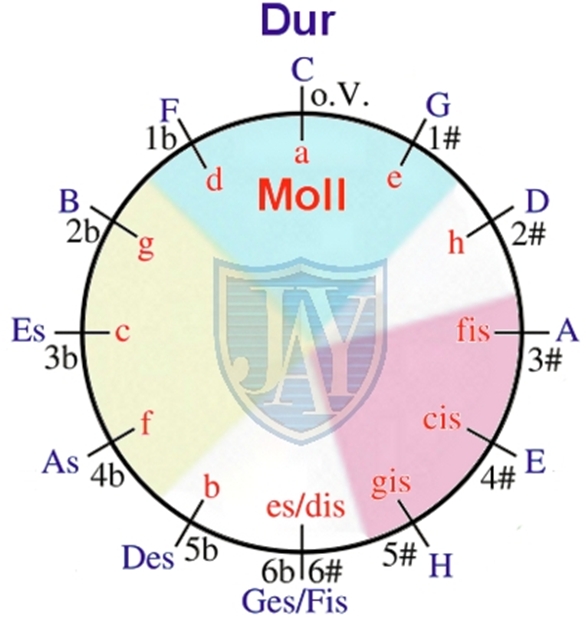
The circle of fifths
This construction"”despised by some, cursed by many and generally underestimated"”contains a host of useful information. It helps us explain the reasons for the different key signatures and which sharps or flats are required where. But that is only one application.
Earlier, we saw that each note can have 2 different names: C#= Db, D#= Eb, and so on. This is called an enharmonic shift.
The circle of fifths’ lowest position (6 o’clock) is called F# major. If one kept adding ever more sharps from that point on (which, though possible in theory, is hardly ever used), there wouldn’t be much left of the notes that make up the C major scale by the time you get back there (C D E F G A B).
We already lost the "F" to G major, the "C" to D major, the "G" to A major, the "D" to E major, the "A" B major, and the E to F# major. And which musician accepts to even look at scores with more than 7 sharps?
Meet the flat signs (b). Following the circle of fifths in the counter-clockwise direction turns it into a circle of fourths, because the interval between the C and F is a fourth.
To build an F major scale without sharps (G major already has a #, and it would become confusing), we need to lower the B to a Bb. That explains why the F major scale uses one b (flat) in its key signature. The fourth interval from the F is precisely that Bb, which also means that Bb major uses 2 flats: one that lowers the B to Bb and a second that lowers the E to Eb. Continuing this system leads us to Gb major, which is actually the same as F# major"”and that’s where we come full circle.

Scales
Let’s add some more confusion by analyzing which other scales can be built from C major.
After all, we could also play the C major scale from D to D, in which case its character somehow seems to change dramatically. That is due to the third note of this scale. While the C and E of the C major scale are separated by two whole tone steps (a major third), the D and Fare only 1 ½ steps apart (minor third).
The third determines whether we are dealing with a major or minor scale. As the name implies, a major third leads to major, while a minor third produces a minor scale. On the other hand, playing the exact same notes of the C major scale, but starting from a different note, turns the scale into a minor scale. Let us use the same scale but now start from the E. This again produces a minor scale but with a slightly different structure than our D minor scale. This shift is due to an asymmetrical sequence of whole and semitone steps.
Here are the technical names:
"Ionian"
"Dorian"
"Phrygian"
"Lydian"
"Mixolydian"
"Aeolian"
"Locrian"
- the slightly "strange" scale that contains a minor third but no pure fifth. You may have come across the term "church mode". Well, the above is all there is to this mystery!
When looking at complete melodies that can be played to specific chords, this information will come in handy. It will also help us making up melodies as we go, something we call "improvisation". The technical terms mentioned above are Greek, by the way, and also used in fine arts: there are indeed ancient column types called Aeolic, Doric and ionic. For European melodies and scales, this is all you need to know. For blues, however, there is some more to talk about ;-)
Obviously, all this theory will only prove useful if you accept to explore and apply it. You probably don’t have to be a pianist, but if there is any way you could purchase a simple keyboard instrument, it would help you visualize the notes and hear them without too much effort.
In the second part, I will discuss the relationship of tones which"”if all goes to plan"”should be rather harmonious, and that is why we call that "harmonies". Any instance of at least two notes sounding together is called a "harmony". And that explains why knowing at least something about them can be beneficial.
Yours,